Introducción
Los conjuntos y las relaciones son el lenguaje en el que se escribe la matemática. Aunque se suelen presentar de manera temprana en la educación, su utilidad no es meramente una herramienta preliminar, sino que son la manera de definir objetos, establecer conexiones entre ellos y organizar teorías enteras.
En este artículo se muestra qué son conjuntos y relaciones formalmente y por qué son tan necesarios para hacer matemáticas.Entenderlos bien evita interpretaciones ingenuas que bloquean el camino para estudiar más adelante funciones, estructuras algebraicas, lógica y computabilidad teórica.
El material está pensado para alumnos de últimos años de secundaria y primeros años de universidad que necesitan una buena base conceptual para adentrarse en terrenos más abstractos. No pretende enseñar técnicas ni recetas, sino crear un marco estructural para entender cómo encajan las piezas (los objetos matemáticos) en un sistema formal.
Marco conceptual
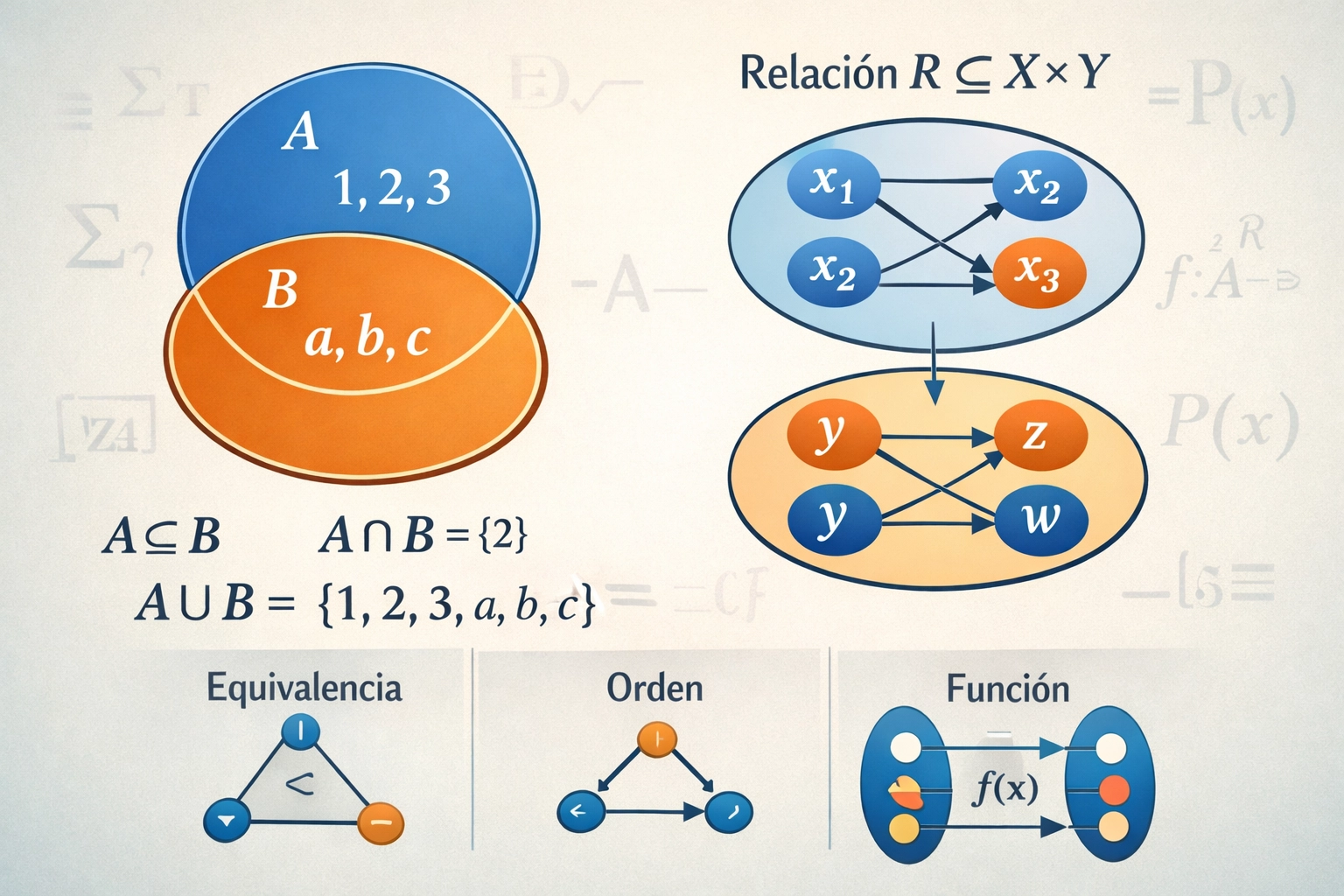
En matemáticas, un conjunto es una colección bien definida de objetos, los cuales son objetos abstractos que quedan definidos dentro de un marco formal. Los conjuntos no son objetos físicos ni empíricos, sino que definen una pertenencia: un elemento pertenece o no al conjunto, sin términos medios.
Una relación es una estructura que especifica cómo se relacionan entre sí los elementos de uno o más conjuntos. Formalmente, una relación se define como un subconjunto del producto cartesiano de conjuntos. Esto permite hablar en términos precisos de asociaciones, correspondencias o dependencias entre elementos, sin necesidad de recurrir a nociones intuitivas.
Formalmente, conjuntos y relaciones no son nociones auxiliares, sino constitutivas del lenguaje matemático, mediante las cuales se definen funciones, órdenes, estructuras algebraicas, sistemas lógicos, etc., sin depender de ejemplos concretos, sino de las definiciones y reglas formales que especifican cómo pueden ser manipulados dentro de un sistema.
Entender esto significa reconocer que las matemáticas trabajan con estructuras abstractas bien definidas, y que todo lo demás se construye a partir de la idea de pertenencia y de la definición formal de relaciones entre elementos.
Estructura y elementos fundamentales
La teoría de conjuntos y de relaciones se basa en ciertos elementos formales que permiten construir y manipular conjuntos y estructuras matemáticas. Estos elementos definen la pertenencia de un objeto a un conjunto, la cual se denota mediante una notación específica. La pertenencia es una relación binaria y excluyente: un objeto o pertenece o no pertenece a un conjunto.
Subconjuntos
Un subconjunto se da cuando todos los elementos de un conjunto están incluidos en otro. Esto permite crear jerarquías y organizar colecciones de objetos matemáticos en estructuras más grandes. El subconjunto es fundamental para definir la igualdad de conjuntos y construir sistemas más complejos.
Conjuntos y operaciones básicas
Sobre los conjuntos se definen operaciones como la unión, la intersección y la diferencia.Estas operaciones no son acciones físicas, sino procedimientos abstractos que crean nuevos conjuntos a partir de otros, siguiendo reglas precisas.
Relaciones y producto cartesiano
Las relaciones se definen a partir del producto cartesiano de conjuntos. El producto cartesiano define un conjunto de pares ordenados, especificando exactamente qué pares (o tuplas) están relacionados. A partir de ahí se definen las relaciones de equivalencia y las relaciones de orden.
Estos conceptos son fundamentales para definir estructuras matemáticas más complejas y por eso la teoría de conjuntos y relaciones es el punto de partida para hacer matemáticas de manera rigurosa.
Ejemplos conceptuales
Para entender la función organizadora de los conjuntos y las relaciones, veamos ejemplos que ilustran cómo definen la igualdad de conjuntos (dos conjuntos son iguales si tienen los mismos elementos, independientemente de cómo se representan), mostrando que la pertenencia, y no la representación, es lo que determina las propiedades formales de un objeto matemático.
Otro ejemplo son las relaciones de equivalencia.Al definir una relación con ciertas propiedades formales, se pueden agrupar en clases todos los elementos que tienen algo en común (sin necesidad de una clasificación empírica), sino en virtud de la relación abstracta que se define en un conjunto.
Un tercer ejemplo son las relaciones de orden, que permiten ordenar los elementos de un conjunto según criterios formales (sin necesidad de una intuición empírica). Las relaciones de orden precisan comparaciones sin ambigüedad, las cuales son la base para construir conjuntos ordenados y espacios matemáticos.
Estos ejemplos ilustran que conjuntos y relaciones no son entidades aisladas, sino instrumentos formales para definir, organizar y manipular estructuras matemáticas.
Errores comunes y malas interpretaciones
El estudio de conjuntos y relaciones a menudo se ve influenciado por interpretaciones erróneas que dificultan comprender su papel estructural en las matemáticas.
Un error común es pensar en un conjunto como una colección física de objetos. Esto confunde la manera intuitiva de hablar de conjuntos con la manera formal. En matemáticas, un conjunto no es una colección física, sino una entidad abstracta definida solo por el criterio de pertenencia.
Otra confusión común es que las relaciones siempre describan conexiones "naturales" o evidentes entre cosas. En realidad, una relación es válida si está bien definida, independientemente de si resulta intuitiva. La formalización es lo que la legitima en matemáticas, no la intuición.
También suelen identificar las relaciones con funciones, ignorando que las funciones son sólo un caso particular dentro de un conjunto mucho mayor de posibles relaciones, lo cual genera errores conceptuales en etapas posteriores del estudio.
Finalmente, muchos estudiantes ven la notación como una barrera artificial en lugar de una herramienta de precisión, lo que lleva a errores de interpretación y a razonamientos vagos. La notación formal no es un adorno: permite eliminar ambigüedades y garantizar la consistencia en el razonamiento.
Superar estas confusiones es necesario para entender por qué la teoría de conjuntos y de relaciones es la base formal de la matemática moderna.
Relación con otros fundamentos matemáticos
La teoría de conjuntos y de relaciones es el fundamento de muchas otras ramas de las matemáticas y un lenguaje para definirlas.
En primer lugar, se conecta con la lógica matemática, ya que muchas nociones lógicas pueden expresarse en términos de conjuntos y relaciones (las proposiciones, los predicados y las estructuras lógicas se definen usualmente en términos de relaciones sobre conjuntos precisos).
En segundo lugar, las funciones se definen en términos de relaciones (una función no es más que una relación con ciertas propiedades adicionales de unicidad y correspondencia), lo que permite manipular las funciones como entidades formales sin necesidad de pensar en sus imágenes gráficas o concretas.La matemática discreta manipula explícitamente conjuntos finitos, relaciones y estructuras asociadas (como grafos o combinatorias) y sin precisar qué son conjuntos y relaciones no se puede hablar rigurosamente de nada de eso.
Finalmente, áreas como la computación teórica o la criptografía definen algoritmos, lenguajes formales o sistemas de seguridad en términos de conjuntos y relaciones y en esos campos no se trata de elegancia, sino de necesidad para poder garantizar la corrección y seguridad de los sistemas.
Estos ejemplos muestran que conjuntos y relaciones no son nociones aisladas, sino el punto de partida formal de toda la matemática moderna.
Importancia del concepto en el estudio de las matemáticas
Dominar los conjuntos y las relaciones es esencial para hacer matemáticas rigurosas, ya que explican cómo se construyen los objetos matemáticos y cómo se enlazan formalmente entre sí; sin ello, todo lo que sigue queda en piezas sueltas sin justificación.
Manejar la teoría de conjuntos permite entender por qué las definiciones siempre deben preceder a los procedimientos y por qué la precisión del lenguaje es tan importante; muchas dificultades en materias como funciones, álgebra abstracta o análisis matemático no se deben a problemas técnicos, sino a no comprender pertenencia, subconjunto y relación.Además, estos conceptos son reutilizados permanentemente en cursos más avanzados, tales como lógica formal, matemática discreta, teoría de la computación, criptografía, etc., en los cuales la corrección de los razonamientos se justifica en términos de estructuras establecidas en términos de conjuntos y relaciones.
Asumir esta perspectiva estructural permite al estudiante elaborar una visión articulada de las matemáticas, evitando manipulaciones intuitivas que no resisten un análisis formal.
Conclusión técnica
Los conjuntos y las relaciones son el lenguaje en que se expresa casi toda la matemática actual; con ellos se definen objetos abstractos, se estructuran y se establecen conexiones precisas entre las cosas, sin necesidad de recurrir a significados empíricos.
En este artículo se ha explicitado el marco conceptual de conjuntos y relaciones, sus elementos y errores comunes que dificultan su comprensión; lo que permite establecer las bases para abordar con rigor nociones posteriores como funciones, estructuras algebraicas y sistemas lógicos.
El manejo de conjuntos y relaciones prepara al estudiante para moverse con precisión en las matemáticas y las ciencias formales, donde la exactitud conceptual y la consistencia estructural son fundamentales.
